EL DESAFIO DEL ELCA!!!

Bueno, hace tiempo que no posteo y es que el estudio y un poco de poker y entremamiento por supuesto esta cansandome un poco.

Les comento que acavo de llegar a los u$s200 y estoy jugando mesas de nl10 y nl20 en cake poker

el objetimo es llegar a llegar a u$s450 en 2meses, osea, 60 dias, posteare dia a dia  como va saliendo la cosa. Si alguien cree que no puedo llegar, pues que me apueste, seguro que va a caer xd

Bueno ahora a lo que le sirve a los lectores, las matematicas basicas del poker y ahora si son muuy muuy importante, asi dejan  de lado "la intuicion" como elemento principal de juicio y lo tiene como refuerzo de matematicas, por que el poker para mi es eso, matematicas, azar.....

bueno aca les dejo un articulo muy bueno y espero que esten llegando a jugar torneos de $0.27 jajja, suerte y dejen sus comentarios.

 

 

Probabilidad - Cálculo de probabilidades

 

Cálculo de probabilidades

Outs

Primeramente definiremos lo que es un out, que no es más que una de las cartas en la baraja que completan nuestra jugada. Por ejemplo, si tenemos una pareja de ases en la mano, tendríamos 2 outs para mejorar a un trío, pues quedan otros 2 ases en la baraja. Si tuviésemos unas dobles parejas, cuatro cartas del mazo nos sirven para completar un full, por lo que tendríamos 4 outs.

Contar nuestras outs

Ahora que sabemos lo que es un out, necesitamos saber contar los que tenemos en cada jugada para evaluar nuestra probabilidad de mejorar. Esto sería muy sencillo si no entrasen en juego nuestros rivales, ya que tan sólo deberíamos contar las cartas que nos ayudan a completar nuestra jugada. Sin embargo, en ocasiones nuestros outs completarán también la jugada de nuestros rivales. Es por eso que debemos saber contar y descontar outs según nuestra mano y las cartas públicas.

Un ejemplo típico es cuando hay dos cartas del mismo palo en la mesa, abriendo la posibilidad de que alguien forme un color. Imaginemos que tenemos 89 en mano, y el flop muestra A56. Cualquier 7 nos da la escalera, pero el 7 posibilita que un jugador complete un color y supere nuestra mano. Por lo tanto contaremos 3 outs, en lugar de los 4 habituales.

Lo mismo sucede con escaleras por debajo, es decir, donde las cartas altas están en la mesa. Por ejemplo, si tenemos 89 en mano, y en el turn las cartas públicas son TQK7, cualquier 6 ó J nos da una escalera. Sin embargo, una J también le da una escalera a cualquiera que tenga un As, y lo que es peor, superior a la nuestra. Por lo tanto, parece obvio que tan sólo deberemos considerar que tenemos 4 outs, uno por cada 6.

Cálculo de probabilidades en el póquer

Ahora que tenemos claro lo que es un out, podemos explicar como se calcula la probabilidad de robar uno de nuestros outs tras el flop. El proceso es muy sencillo. Una baraja de póquer tiene 52 cartas, 13 por palo. Hemos visto 2 en mano, más las 3 del flop, por lo que quedan 47 cartas sin ver en la baraja (para los cálculos suponemos que jugamos sólo nosotros).

Si continuamos con el ejemplo de la pareja de ases, donde teníamos 2 outs, quiere decir que 2 de las 47 cartas restantes en el mazo completan nuestra jugada. De tal forma, para calcular el porcentaje de veces que completaremos nuestra jugada en la siguiente carta tan sólo debemos dividir 2 entre 47 y multiplicarlo por 100.

Probabilidad = [Numero de outs / Cartas en la baraja] * 100 

Probabilidad de completar un trío en el turn = 2/47*100=4.25%

Este resultado es la probabilidad de robar uno de nuestros dos outs en el turn. Para evaluarla en el river, tan sólo deberíamos repetir la fórmula pero con una carta menos en la baraja.

Probabilidad de completar un trío en el river = 2/46*100=4.35%

Por ahora sabemos lo que es un out, contar los mismos, y calcular la probabilidad de conseguir nuestra jugada a una carta vista. De momento el principiante no necesita más para pasar al siguiente punto.

Probabilidad - Odds

Odds, otra forma de expresar la probabilidad

Existe otra forma para expresar la probabilidad de que ocurra un suceso, más adecuada para el póquer u otros juegos de cartas, denominada en inglés odds. Es un formato de dos números separados por dos puntos. El primero indica la probabilidad de que el suceso no ocurra, y el segundo las probabilidad de que ocurra. La suma de ambos es el total de intentos del suceso.

Pongamos un ejemplo. La probabilidad de que en un lanzamiento de un dado salga un 6 es apróximadamente de un 16% ó 1/6. Esta probabilidad expresada en odds equivale a 5:1. Por cada 6 veces que lanzemos el dado, 5 saldrá distinto de 1, y una vez saldrá el 1. Por lo tanto, 16%, 1/6 y 5:1 son formas equivalentes de expresar la misma probabilidad.

Cálculo de odds

Pasos a seguir para hayar la probabilidad de una jugada de póquer expresada en odds.

1. Contar las outs que tenemos.
2. Restar nuestras outs al número total de cartas en la baraja. Este número será el número de cartas que no completan nuestra jugada.
3. Expresar las odds de la forma [cartas que no completan nuestra jugada : outs]
4. Dividir la expresión anterior entre el número de outs.

Pongamos un ejemplo

Pongamos un ejemplo. Supongamos que tenemos en mano 67, y en el turn, el tapete muestra 9A2Q. Para calcular nuestras odds de completar un color tan sólo debemos seguir los pasos anteriores.

1. Nuestas outs son los 9 diamantes que quedan en la baraja.
2. Si estamos en el turn quedan 46 cartas por ver, por lo que el número de cartas que no nos sirve será 46 - 9 = 37.
3. Formamos la expresión 37:9 (debe sumar 46).
4. Dividimos entre 9 para obtener 4.1:1.

Es decir, 1 de cada 5.1 veces completaremos nuestro color en el river, o lo que es lo mismo en un 20% aproximado de las ocasiones.

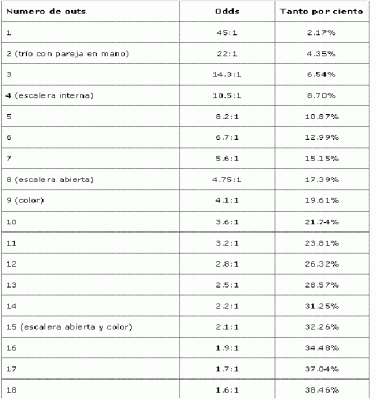
La tabla de odds

Ahora bien, ¿un jugador de póquer hace todos estos cálculos cada vez que debe decidir si debe jugar o no una mano? Decididamente no. Afortunadamente disponemos de unas tablas de odds donde encontramos resumidas todas las probabilidades, de tal forma que el único cálculo que debemos hacer es contar nuestras outs. Esta tabla que veremos a continuación, es lo único que deberías memorizar en tu carrera de jugador, si bien, jugar online tiene ventajas como poder tenerla delante siempre para consultarla.

Algunas jugadas frecuentes

El proceso de contar las outs, también es bastante sencillo, pero conviene que tengamos en cuenta los outs de algunas jugadas frecuentes como son:

Proyecto de color (4 cartas del mismo palo) 9 outs
Proyecto de escalera acierta 8 outs
Proyecto de escalera interna 4 outs

Puesto que ya sabemos comprender el formato de odds para expresar una probabilidad, y hemos visto como apoyarnos en la tabla de odds para simplificar nuestros cálculos pasaremos a ver un nuevo concepto necesario para elegir correctamente nuestras acciones.

 

Probabilidad - Pot odds

Pot odds, o odds que nos ofrece el bote

Definamos en primer lugar el concepto de pot odds, que no es más que las relación entre el tamaño del bote y el de nuestra apuesta. Por ejemplo, si en el bote hay 20$ en el turn, en una mesa de 1/2$, el bote nos está ofreciendo unas pot odds de 10:1. Si en el bote hubieran 10$ nuestras pot odds serían de 5:1. Es decir, para calcular las pot odds, tan sólo debemos dividir el tamaño del bote, entre el tamaño de nuestra apuesta.

¿Para que sirven las pot odds?

Principalmente lo usaremos en las situaciones en las que necesitemos robar una determinada carta para llevarnos el bote. Si la relación entre lo que debemos apostar y el tamaño del bote, las pot odds, es menor que nuestras odds de completar la jugada, nuestra apuesta tiene expectativa positiva en el largo plazo. Si por el contrario, las pot odds, son mayores que nuestras odds, deberemos abandonar pues la apuesta tiene expectativa negativa.

Recordaré que las pot odds son menores, si el primer número es mayor que el de nuestras odds. Por ejemplo, unas pot odds de 9:1 son menores que 5:1. El primer dato equivale a una de cada diez veces o 10%, mientras el segundo a una de cada seis o 16%.

Un par de ejemplos

Estamos jugando una mano en una mesa de 1/2$. Imaginemos que en el bote hay 8$ al comenzar el turn, y tenemos un proyecto de color en última posición. En la mesa quedamos 3 jugadores. El primero de ellos apuesta, mientras el segundo abandona. Llega nuestro turno. ¿Debemos ver o no la apuesta de nuestro rival? Es en este momento cuando debemos calcular nuestras odds y compararlo con las pot odds que nos ofrece el bote.

Como hemos visto anteriormente, tenemos 9 outs para completar nuestro color, lo que nos da unas odds de 4.1:1. En el bote hay 10$, contando la apuesta de nuestro oponente en el turn, es decir, nuestras pot odds son de 5:1. Por lo tanto, como la relación entre lo que tenemos que aportar al bote es menor que nuestras odds de completar la jugada, podemos ver la apuesta con una expectativa favorable.

Examinemos la situación en detalle. Nuestras odds, de 4.1:1 nos indican que por cada 5 veces que realizemos esta apuesta, en 4 de ellas perderemos 2$ (en total 8$) y una quinta ganaremos 10$ (el bote), lo que nos da un beneficio neto de 2$. Es por ello que nuestra apuesta es rentable en el largo plazo, y por lo tanto deberemos ver.

Ahora imaginemos la misma situación, pero el segundo rival sube la apuesta en lugar de abandonar. En ese caso nuestras odds de completar la jugada son las mismas, 4:1, sin embargo nuestras pot odds se ven reducidas a la mitad. Veámoslo.

En el momento de actuar el bote tiene 14$, los 12$ iniciales más una apuesta y un raise del segundo jugador. Para continuar en la mano debemos aportar 4$ al bote, en lugar de los 2$ anteriores, por lo que nuestras pot odds pasan a ser de 3.5 (debemos aportar 4$ a un bote de 14$, 14/4=3.5). Por lo tanto, nuestras odds son menores que las que nos ofrece el bote, y no debemos apostar pues a la larga perderemos dinero al tener una expectativa negativa.

Si examinamos la jugada detenidamente como en el primer ejemplo, podemos ver las implicaciones negativas de nuestra apuesta. En el bote hay 14$, y nuestras odds de completar el colo nos dicen que una de cada cinco veces ganaremos un bote de 14$, mientras que en las otras cuatro perderemos 4$ que hacen un total de 16$. Por lo tanto nuestro call tiene una expectativa de -2$. Perderemos dinero cada vez que lo vemos esta apuesta.

Como nota al margen, fijaros en la importancia de la acción de subir del segundo jugador. Subiendo ha convertido nuestra mano de favorable matematicamente a no favorable. De esta forma él protege su mano ante proyectos como el nuestro, en el caso de que hagamos lo correcto y no le veamos. Si no tenemos en cuenta las odds y le viésemos, él gana dinero igualmente, pues estás apostando contra tus odds. Esto es sólo un ejemplo del potencial de la acción de subir que trataremos con detenimiento más adelante en Póquer-Red.

Reduciendo tus pot odds según tu posición relativa

Este es otro ejemplo de la importancia de la posición en el hold’em. En este caso no nos importa nuestra situación en la mesa, sino la posición del agresor, del oponente que apuesta. En general, si apuesta a nuestra derecha y quedan más oponentes por actuar, nos podemos enfrentar a una posible subida de algunos de los rivales que hablan después de nosotros. Si la apuesta viene desde nuestra izquierda, probablemente cerraremos la ronda de apuestas teniendo mucha información disnponible.

Por ejemplo, imagina que juegas en una mesa de 1/2$. El bote tiene 12$ y te encuentras en segunda posición. Quedan 3 oponentes y el primero de ellos apuesta. Tus pot odds son de 7:1, con lo que si por ejemplo tuvieras 6 outs con cartas altas, deberías ver pues tus odds serían de 6.7:1. Sin embargo, si alguno de los que quedan por hablar sube la apuesta, tus pot odds se reducen considerablemente.

En el bote habrían 20$, los 12$ iniciales, más la apuesta del primer rival, tu call, y el raise del tercer jugador. Como para ver debes aportar 2$ extra, tus pot odds iniciales han pasado a ser de 5:1 (4$ para un bote de 20$). Del mismo modo, si el primer jugador vuelve a subir en su turno, tus pot odds se reducen todavía más hasta ser de 4:1 (6$ para un bote de 24$).

Por lo tanto, si prevees que en un bote vaya a ver mucha acción por como se ha desarrollado la mano, reduce tus pot odds de forma considerable y juega sólo tus mejors manos. Mejor ser conservador que verse envuelto en una guerra en la que tienes pocas opciones. La noche es larga y quedan muchas manos por jugar.

 

 

Probabilidad - Odds implícitas

Las pot odds no tienen en cuenta las apuestas que puedan darse tras la ronda en la que nos encontremos, por lo que necesitamos del concepto de odds implícitas para poder evaluar estas apuestas extras que podemos ganar. Las odds implícitas serán las pot odds ajustadas para las siguientes rondas de apuestas.

Imaginemos una mano en una mesa de 1/2$ donde tenemos 68 en mano en la ciega grande. En el turn, quedas sólo tú contra un rival en primeras posiciones. Las cartas comunes son 59A2, por lo que tenemos un proyecto a una escalera interna con 4 outs, los 4 sietes que completan nuestra jugada. Pasamos en el turn, y nuestro rival apuesta, elevando el bote a 18$. ¿Debemos ver su apuesta?

Si consultamos la tabla de odds, vemos que nuestra jugada tiene unas odds de 10.5:1, mientras que las pot odds que nos ofrece el bote son de 9:1. Con lo visto hasta ahora, sabemos que ver la apuesta de nuestro rival tiene una expectativa negativa, por lo que no deberíamos ver. Ahora bien, ¿que sucederá en el turn si completamos nuestra escalera?. Nuestro rival probablemente está apostando con un As o algo superior. Si pasamos en el river, con seguridad nos apostará intentando sacarnos una apuesta extra, a lo que nosotros responderemos resubiendo.

Por lo tanto, nuestro call en el turn de 2$ en el turn, tiene un beneficio extra las veces que completemos nuestra jugada, mientras que cuando no lo completamos abandonamos sin ningún coste adicional. De esta forma podemos ajustar el tamaño del bote añadiendo las apuestas que esperamos ganar en el river. En esta jugada, añadimos 2 apuestas grandes, lo que hace un bote de 22$, elevando nuestras pot odds a 11:1 y convirtiendo nuestro fold en un call.

Un buen ejemplo de como jugar una mano por el beneficio extra que conseguimos cuando completamos nuestra jugada lo encontramos en el magnífico libro de David Sklansky, Theory of poker. En él explica el caso de las parejas pequeñas, que frecuentemente jugamos por sus odds implícitas. Estas parejas tienen un 7.5:1 de mejorar a un trío en el flop, pero sin embargo, podemos jugarlas preflop con tan sólo unas pot odds de 5:1 por el tremendo beneficio que conseguimos en las ocasiones que completamos el trío.

Un factor clave a la hora de calcular nuestras odds implíctas es cuán oculta está nuestra mano. No suma lo mismo una jugada como la vista en el ejemplo anterior, en la que saliendo un 7 en el river, nuestro rival no espera que completemos ninguna mano, que una donde la carta que necesitemos asuste a cualquiera. Por ejemplo, si tenemos A5 en un flop 89QA, no esperemos que nuestro rival suba si aparece un corazón en el river. Nuestras odds implícitas disminuyen.

Del mismo modo, cuanto peor el jugador, más odds implícitas podemos sumar ya que podemos contar con que jugando peor va a pagarnos más por nuestras manos. Un ejemplo de mal jugador sería el que apostase en el flop anterior saliendo un corazón en el river.

En general las odds implícitas, deberemos calcularlas cuando estemos convencidos que completando la jugada a la que robamos, nos llevaremos el bote. Si tenemos una segunda mejor mano, que aún mejorando puede quedar segunda, es mejor no sólo no contar sus odds implícitas, sino descontar odds. Es lo que se denominan odds implícitas reversas. De esta forma, limitamos jugar estas segundas mejores manos, a botes gigantes en donde las pot odds sean tan grandes que valga la pena el intento. Para botes pequeños no dudes en descontarte odds y abandonar sin remordimientos.